对于互联网上的所有敏感活动而言,都必须运用密码学。服务器通信必须像数据存储一样安全。
密码学(一种机密通信科学)可以解决此难题。“密码学”一词的语源来自希腊语中的“crypto”,它表示“隐藏”或“机密”,而“Graphy”表示绘制、编写或描述的方法或形式。
随着网上投注和互联网安全需求的增加,密码学已变成一项多方面的学科。使用加密法作为对内容进行加密的方法或算法只是密码学的一项功能。除此之外,加密法必须能够抵御窃听者、所选纯文本攻击和所选密文攻击并确保以下任意项:
机密性:定义为保持机密的意向。
完整性:一种确认无数据损坏的方法。
身份验证:一种证明您与之通信的设备所声称的内容属实且不是第三方攻击程序的方法。
授权:对执行操作所需的权限的适当分配。
现代密码学在第二次世界大战后发展起来。1949 年,Claude Shannon 对理论安全背后的信息进行了概念化。他的基本理念是:密文应不揭露任何有关纯文本的信息。在数学中,通过此方式编写密文:
Shannon 实施的完全保密
∀ 消息 m0 和 m1 ϵ M(所有消息的空白),例如 length(m0) = length(m1) 和 ∀ c ϵ C(所有密文的空白)
Pr[E(k, m0) = c] = Pr[E(k,m1) = c]
其中,k 在 K(所有密钥的空间)中是一致的
换句话说,在提供密文的情况下,攻击者无法告知加密的消息是针对所有可能的 m0 和 m1 消息的 m0 或 m1,因此,甚至最强有力的对手也无法从密文中获得任何有关纯文本的信息,从而无法发起密文攻击。
在我们的数字世界里,密码技术是通过计算机实施的。XOR 逻辑函数是加密算法的基本构建块,这是因为它具有一个由以下定理表示的重要性质:
如果 Y 是 {0,1}n 上的随机变量,而 X 是 {0,1}n 上的独立一致变量,则 Z = Y XOR X 为 {0,1}n 上的一致变量
这将阻止频率分析(它是 20 世纪中期之前所使用的方法的缺点)。
一次性密钥算法
一次性密钥 (OTP) 是一种算法,它采用消息 m 和密钥 k(m 和 k 的长度相同)以及 XOR m 和 k。由于 k 是一致变量,因此 Z 也是一致变量,并且窃听者无法执行任何密文攻击。遗憾的是,要实施完全保密,密钥必须长于消息 (|K| > |M|),这在实践中几乎是不可能的。的确,如果我们获得两条具有相同密钥 k 的加密消息,则对这两条密文进行 XOR 处理将生成 m1 XOR m2,,并且对此结果进行简单统计分析可发现大量有关纯文本的信息。
要使 OTP 切实可行,可将随机密钥替换为“伪随机”密钥,并理解:即便获知所有之前生成的密钥,发现新密钥的可能性也微乎其微 (≤1/280)。 此外,不讨论用于描述 Shannon 的完全保密的完全均等,假定我们在 2 个密文具有不能区分的分布的情况下拥有语义安全性,我们将再次谈论概率。密钥生成是实现良好安全性的基础。WEP 协议表明,密钥中的错误选择会降低安全性。
WEP 是不安全的,因为 IV(初始化向量)的长度为 24 位,这意味着约每 1600 万帧使用一次相同的密钥。此外,密钥也是相关的;帧 1 的密钥为 1||k,帧 #2 的密钥为 2||k。此外,IV 会在重启后重置为 0,使得攻击者能够在仅 40,000 个帧后恢复密钥,这在如今的环境中是绝对不安全的。要弥补这个缺陷,在网络流量中,必须为每个会话商定一个新的密钥。在现代流密码中,种子 + 随机数(给定密钥的非重复值)用于生成密钥,并且绝不会使用对(种子,随机数)一次以上。这些流密码中最有名的是 RC4、Salsa 或 Sosemanuk。
请记住,OTP 非常适用于网络中的通信,但不是很适合数据存储。的确,OTP 不具有完整性,因为它是可变的 - 这意味着,对密文的修改是检测不到的并会对纯文本产生可预测的影响。
块密码
块密码是另一种加密方法。虽然块密码实施起来比流密码更复杂且更慢,但它更可靠并且能够解决流密码遗留的难题。与流密码不同,块密码是一个包含 n 位的固定块,经过打乱重组后创建 n 位的密文。如果消息少于 n 位,则需要填补消息以达到 n 位。AES 和 RSA 是最常见的块密码加密。
对于块密码,提供以下 2 种操作模式:CBC(密码块链接)模式和 CTR(计数器)模式。每种模式均需要一个 IV(初始向量)才能开始加密,但随后的实现会有差异。与采用并行实现的 CTR 模式不同,CBC 模式采用串行实现。
此处采用 CBC 模式进行加密:选择一个随机 IV,然后每个块的输出将用于加密下一个块。

此处采用 CTR 模式进行加密:F 为伪随机函数,IV 对于每条消息都是随机的,而对于每个块是递增的。F 可并行应用于每个块。

所有这些方法都能有效防止窃听者并确保机密性,但任何方法都不能确保完整性、身份验证和抵御主动攻击。
消息认证码
消息完整性基于 MAC(消息认证码)。标记基于消息 m 和密钥 k 而生成。接收方在收到消息后可执行验证标记,其中输出为“是”或“否”。MAC 计算使用 PRF(伪随机函数),因此攻击者无法为新消息生成有效的标记。完整性需要密钥,但不要与 CRC(循环冗余码)混淆,后者旨在检测随机的、非恶意错误。
流密码和块密码可构建机密性(换言之,它们可有效防止窃取,但无法有效防止主动攻击),而 MAC 可确保完整性而非机密性。但如果对密文执行 MAC,则将以认证加密结束。攻击者无法创建已正确解密的新密文。随后可执行完整性、身份验证和授权。
所有这些方法对发送方和接收方使用相同的密钥,并且被称为“对称加密”。我们假定在通信开始前已交换密钥,但在当今靠互联网连通的世界里,许多人必须在互不相识的情况下交换数据,因而无法先交换密钥。非对称加密是解决此问题的方法。Diffie-Hellman 协议可帮助解释:
如果 p 是一个较大的质数,g 是一个整数 {1,…,p} and x is chosen randomly in {1,…, p-1},并且已知道结果,但没有计算 x 的已知有效算法。然后,使用 x 和 y 这两个数字,可很轻松地执行指数运算来以一个密钥结束,但很难进行逆运算以发现密钥。
g^(x^y ) (mod p)=g^(y^x ) (mod p)= g^xy (mod p) = 用于加密的密钥
如果 Alice 和 Bob 需要共享该密钥,并且他们之间存在一个窃听者,则可执行以下步骤来共享该密钥。
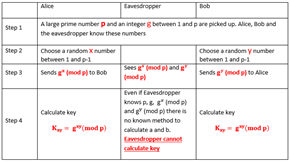
还有多个 Diffie-Hellman 变量,例如椭圆曲线的分解式,形式为:y² = x³ + ax + b。
最后,尽管做出了所有这些努力,仍无法确保安全通信。Shannon 定理从学理的角度论证了完全安全,但实际上来说,旁路攻击是非常强大的。举例来说,2013 年发生了一次绝佳的旁路攻击,那时,研究人员通过在解密 4096 位 RSA 算法的同时侦听计算机 CPU 发出的尖音(10 至 150 kHz)来破解了世界上最难的加密。Daniel Genlin、Adi Shamir 和 Eran Tromer 那时已能够使用这种未知的类型制作解密密钥,这是完全无法预想到的。


